“Can you give me a simple, concrete explanation of how quantum computers work?”
I’ve been asked this question a lot. I worked on quantum computing full time for 12 years, wrote 60 or so papers, and co-authored the standard text. But for many years the question stumped me. I had several pat answers, but none really satisfied me or my questioners.
It turns out, though, that there is a satisfying answer to the question, which anyone can understand if they’re willing to spend some time concentrating hard.
To understand the answer, let’s back up and think first about why big media outlets like the New York Times and the Economist regularly run stories about quantum computers.
The reason is that quantum computer scientists believe quantum computers can solve problems that are intractable for conventional computers. That is, it’s not that quantum computers are like regular computers, but smaller and faster. Rather, quantum computers work according to principles entirely different than conventional computers, and using those principles can solve problems whose solution will never be feasible on a conventional computer.
In everyday life, all our experience is with objects which can be directly simulated by a conventional computer. We don’t usually think about this fact, but movie-makers rely on it, and we take it for granted – special effects are basically just rough computer simulations of events that would be more expensive for the movie makers to create in real life than they are to simulate inside a computer. Much more detailed simulations are used by companies like Boeing to test designs for their latest aircraft, and by Intel to test designs for their latest chips. Everything you’ve ever seen or done in your life – driving a car, walking in the park, cooking a meal – all these actions can be directly simulated using a conventional computer.
Because of this, when we think in concrete terms we invariably think about things that can be directly simulated on a conventional computer.
Now, imagine for the sake of argument that I could give you a simple, concrete explanation of how quantum computers work. If that explanation were truly correct, then it would mean we could use conventional computers to simulate all the elements in a quantum computer, giving us a way to solve those supposedly intractable problems I mentioned earlier.
Of course, this is absurd! What’s really going on is that no simple concrete explanation of quantum computers is possible. Rather, there is an intrinsic quantum gap between how quantum computers work, and our ability to explain them in simple concrete terms. This quantum gap is what made it hard for me to answer people’s requests for a concrete explanation. The right answer to such requests is that quantum computers cannot be explained in simple concrete terms; if they could be, quantum computers could be directly simulated on conventional computers, and quantum computing would offer no advantage over such computers. In fact, what is truly interesting about quantum computers is understanding the nature of this gap between our ability to give a simple concrete explanation and what’s really going on.
This account of quantum computers is distinctly at odds with the account that appears most often in the mainstream media. In that account, quantum computers work by exploiting what is called “quantum parallelism”. The idea is that a quantum computer can simultaneously explore many possible solutions to a problem. Implicitly, such accounts promise that it’s then possible to pick out the correct solution to the problem, and that it’s this which makes quantum computers tick.
Quantum parallelism is an appealing story, but it’s misleading. The problem comes in the second part of the story: picking out the correct solution. Most of the time this turns out to be impossible. This isn’t just my opinion, in some cases you can mathematically prove it’s impossible. In fact, the problem of figuring out how to extract the solution, which is glossed over in mainstream accounts, is really the key problem. It’s here that the quantum gap lies, and glossing over it does nothing to promote genuine understanding.
None of my discussion to now actually explains how quantum computers work. But it’s a good first step to understanding, for it prepares you to expect a less concrete explanation of quantum computers than you might at first have hoped for. I won’t give a full description here, but I will sketch what’s going on, and give you some suggestions for further reading.
Quantum computers are built from “quantum bits”, or “qubits” [1], which are the quantum analogue of the bits which make up conventional computers. Here’s a magnified picture of a baby quantum computer made up of three Beryllium atoms, which are used to store three qubits:
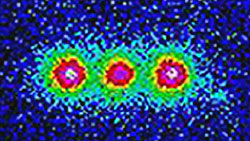 (credit to the NIST trapped ions group)
(credit to the NIST trapped ions group)The atoms are held in place using an atom trap, which you can’t see because it’s out of frame, but which surrounds the atoms, holding them suspended in place using electric and magnetic fields, similar to the way magnets can be used to levitate larger objects in the air.
The atoms in the picture are about three micrometers apart, which means that if you laid a million end to end, they wouldn’t quite span the length of a living room. Very fine human hair is about 20 micrometers in diameter – it’d pretty much cover the width of this photo.
The atoms themselves are about a thousand times smaller than the spacing between the atoms. They look a lot bigger in the picture, and the reason is interesting. Although the atoms are very small, the way the picture was created was by shining laser light on the atoms to light them up, and then taking a photograph. The particles making up the laser light are much bigger than the atoms, which makes the picture come out all blurry; the photo above is basically a very blurry photograph of the atoms, which is why they look so much bigger than they really are.
I called this a baby quantum computer because it has only three qubits, but in fact it’s pretty close to the state of the art. It’s hard to build quantum computers, and adding extra qubits turns out to be tricky. Exactly who holds the record for the most qubits depends on who you ask, because different people have different ideas about what standards need to be met to qualify as a genuine quantum computer. The current consensus for the record is about 5-10 qubits.
Okay, a minor alert is in order. I’ve tried to keep this essay as free from mathematics as possible, but the rest of the essay will use a little high-school mathematics. If this is the kind of thing that puts you off, do not be alarmed! You should be able to get the gist even if you skip over the mathematical bits.
How should we describe what’s inside a quantum computer? We can give a bare-bones description of a conventional computer by listing out the state of all its internal components. For example, its memory might contains the bits 0,0,1,0,1,1, and so on. It turns out that a quantum computer can also be described using a list of numbers, although how this is done is quite different. If our quantum computer has n qubits (in the example pictured above n = 3), then it turns out that the right way to describe the quantum computer is using a list of 2n numbers. It’s helpful to give these numbers labels: the first is s1, the second s2, and so on, so the entire list is:
What are these numbers, and how are they related to the n qubits in our quantum computer? This is a reasonable question – in fact, it’s an excellent question! Unfortunately, the relationship is somewhat indirect. For that reason, I’m not going to describe it in detail here, although you can get a better picture from some of the further reading I describe below. For us, the thing to take away is that describing n qubits requires 2n numbers.
One result of this is that the amount of information needed to describe the qubits gets big really quickly. More than a million numbers are needed to describe a 20-qubit quantum computer! The contrast with conventional computers is striking – a conventional 20-bit computer needs only 20 numbers to describe it. The reason is that each added qubit doubles the amount of information needed to describe the quantum computer [2]. The moral is that quantum computers get complex far more quickly than conventional computers as the number of components rises.
The way a quantum computer works is that quantum gates are applied to the qubits making up the quantum computer. This is a fancy way of saying that we do things to the qubits. The exact details vary quite a bit in different quantum computer designs. In the example I showed above, it basically involves manipulating the atoms by shining laser light on them. Quantum gates usually involve manipulating just one or two qubits at a time; some quantum computer designs involve more at the same time, but that’s a luxury, it’s not actually necessary. A quantum computation is just a sequence of these quantum gates done in a particular order. This sequence is called a quantum algorithm; it plays the same role as a program for a conventional computer.
The effect of a quantum gate is to change the description s1, s2,… of the quantum computer. Let me show you a specific example to make this a bit more concrete. There’s a particular type of quantum gate called a Hadamard gate. This type of gate affects just one qubit. If we apply a Hadamard gate to the first qubit in a quantum computer, the effect is to produce a new description for the quantum computer with numbers t1, t2,… given by
t1 = (s1+s2n/2+1)/√ 2
t2 = (s2+s2n/2+2)/√ 2,
t3 = (s3+s2n/2+3)/√ 2,
and so on, down through all 2n different numbers in the description. The details aren’t important, the salient point is that even though we’ve manipulated just one qubit, the way we describe the quantum computer changes in an extremely complicated way. It’s bizarre: by manipulating just a single physical object, we reshuffle and recombine the entire list of 2n numbers!
It’s this reshuffling and recombination of all 2n numbers that is the heart of the matter. Imagine we were trying to simulate what’s going on inside the quantum computer using a conventional computer. The obvious way to do this is to track the way the numbers s1, s2,… change as the quantum computation progresses. The problem with doing this is that even a single quantum gate can involve changes to all 2n different numbers. Even when n is quite modest, 2n can be enormous. For example, when n = 300, 2n is larger than the number of atoms in the Universe. It’s just not feasible to track this many numbers on a conventional computer.
You should now be getting a feeling for why quantum computer scientists believe it is infeasible for a conventional computer to simulate a quantum computer. What’s really clever, and not so obvious, is that we can turn this around, and use the quantum manipulations of all these exponentially many numbers to solve interesting computational problems.
I won’t try to tell that story here. But if you’re interested in learning more, here’s some reading you may find worthwhile.
In an earlier essay I explain why conventional ways of thinking simply cannot give a complete description of the world, and why quantum mechanics is necessary. Going a little further, an excellent lay introduction to quantum mechanics is Richard Feynman’s QED: The Strange Theory of Light and Matter. It requires no mathematical background, but manages to convey the essence of quantum mechanics. If you’re feeling more adventurous still, Scott Aaronson’s lecture notes are a fun introduction to quantum computing. They contain a fair bit of mathematics, but are written so you can get a lot out of them even if some of the mathematics is inaccessible. Scott and Dave Bacon run excellent blogs that occasionally discuss quantum computing, and their blogrolls are a good place to find links to other quantum bloggers.
Finally, if you’ve enjoyed this essay, you may enjoy some of my other essays, or perhaps like to subscribe to my blog. Thanks for reading!
Acknowledgements
Thanks to Jen Dodd and Kate Nielsen for providing feedback that greatly improved early drafts of this essay.
About the author
Michael Nielsen is a writer living near Toronto, and working on a book about The Future of Science. If you’d like to be notified when the book is available, please send a blank email to the.future.of.science@gmail.com with the subject “subscribe book”. You’ll be emailed to let you know when the book is to be published; your email address will not be used for any other purpose.
Footnotes
[1] Ben Schumacher, who coined the term “qubit”, runs an occasional blog.
[2] Motivated by this observation, in my PhD thesis I posed a tongue-in-cheek quantum analogue of Moore’s Law: to keep pace with conventional computers, quantum computers need only add a single qubit every two years. So far, things are neck and neck.

