The Babylonian
Map of the World is one of the world's oldest extant maps, dating
to 600 BCE. It's a crude map, difficult to read at a glance, but
fortunately an accompanying cuneiform text describes the features on
the map, including Babylon, seven other cities, a canal, and a
mountain:
Modern maps are,
of course, far better than this early map. They improve on it by
taking advantage of the many map-making techniques developed since 600
BCE, such as: surveying to get proportions correct; projections to
correct for the curvature of the Earth; methods to depict topographic
features; and so on. Even ideas such as showing roads and nautical
routes were not a priori obvious, but had to be invented.
This agglomeration of ideas has turned maps into a powerful medium
for thought. Consider the famous map of the London Underground,
excerpted here:
Using this map, an
ordinary person can walk into the Underground for the first time, and
within minutes know how to find their way from place to place.
Without the map, with only purely verbal representations to learn
from, even a geographic genius would require days of work to acquire a
similar facility. What's more, we internalize the map: the
representations used in the map become the representations we use to
think about the Underground. This is the sense in which this map is a
medium for thought.
We usually take such media for granted, and rarely pause to think
about the origin of the ideas behind media such as the Underground
map. But those ideas are not obvious, they had to be invented,
usually through a conscious process of design. To better understand
that design process, consider the following prototype
by Bret Victor, one of the
world's great designers of media for thought. It's a medium for
understanding a special class of mathematical equations known as
difference equations, in much the same way as maps help us understand
geography. The video moves fast, but don't worry if you don't follow
it all -- it's the broad approach that I want you to focus on. You
may find the video easier to watch if it's fullscreened, which you can
achieve by clicking the four-arrow icon in the bottom right of the
video player:
It's tempting to evaluate this prototype as a potential user. But
it's a prototype, not a complete product, and if you evaluate it as a
potential user, you're likely to concentrate mostly on its
shortcomings, and miss its virtues. I want you to flip your thinking
around. I want you to think about this as though you are a designer,
and in particular, someone who designs media for thought. From this
point of view, you see immediately that Victor's prototype enables
many powerful operations, such as: tying parameters together; the
instantaneous feedback between symbolic and graphical views of
difference equations; and the language for searching over functions.
He's created a vocabulary of operations which can be used to
understand and manipulate and, most crucially of all, play
with difference equations. And with enough exposure to this medium,
we'd begin internalizing these operations: we'd begin to think about
difference equations in this way.
Once we see media for thought as something that can be consciously designed, the natural question is: how far can we go? What are the most powerful representations and operations we can find? We shouldn't think of this prototype in isolation, but rather as a single step in an open-ended creative process. Imagine creating hundreds of such prototypes, covering many different aspects of a broader subject, such as mathematics. Such prototypes could birth a medium for mathematics far more powerful than existing tools, like Mathematica and Matlab.
In the remainder of this essay I will focus on the design of a particular type of media for thought, namely, the design of media to explain scientific ideas. To make the discussion concrete, I will focus on media to explain a single scientific idea, a result from statistics known as Simpson's paradox. If you've never heard of Simpson's paradox before, you're in for a treat: it's a marvellous result, simple but striking, something every educated person in the world can delight in learning. For us, though, Simpson's paradox serves primarily as a stalking horse. We will use it as a spur to create explanations which go beyond the verbal and symbolic explanations conventionally used to explain science and mathematics. In particular, we shall design a series of prototype explanations that take advantage of media forms including visualizations, television, and video games. These prototypes will be simple and crude, but have the considerable virtue of teaching us something about how to use non-traditional media to create deeper explanations of scientific ideas.
Why go the trouble of constructing these prototypes? My own personal conviction is that we are still in the early days of exploring the potential that modern media -- especially digital media -- have for the explanation of science. Our current attempts at digital explanation seem to me to be like the efforts of the early silent film-makers, or of painters prior to the Florentine Renaissance. We haven't yet found our Michaelangelo and Leonardo, we don't yet know what is possible. In fact, we don't yet have even the basic vocabulary of digital explanation. My instinct is that such a vocabulary will be developed in the decades to come. But that is far too big a goal to attack directly. Instead, we can make progress by constructing prototypes, and learning from what they have to tell us. That's what we'll do in this essay.
A word on what the essay is not. Media such as visualizations, television, and video games are often regarded by scientists mainly as vehicles for popularization. "Serious" scientific explanations are restricted to lectures, papers, and textbooks -- all media based on traditional verbal and symbolic representations. But this essay is most emphatically not about how to popularize Simpson's paradox. Instead, it's about understanding the potential of non-traditional media for serious explanations, the sort of explanations scientists use amongst themselves. So while it happens to be true that the explanations we'll discuss are accessible to a broad audience, what matters is that those explanations are, in some important ways, deeper than conventional verbal and symbolic explanations.
Simpson's paradox: a basic written explanation
Suppose you're suffering from kidney stones and go to see your doctor. The doctor tells you two treatments are available, treatment A and treatment B. You ask which treatment works better, and the doctor says "Well, a study found that treatment A has a higher probability of success than treatment B."
You start to say "I'll take treatment A, thanks!", when your doctor interrupts: "But the same study also looked to see which treatment worked better, depending on whether patients had large kidney stones or small kidney stones." You say "Well, do I have large kidney stones or small kidney stones"? As you speak the doctor interrupts again, looking sheepish, and says "Actually, it doesn't matter. You see, they found that treatment B has a higher probability of success than treatment A, regardless of whether you have large or small kidney stones."
You may wonder if you read that right. It sounds impossible. But it's true: an actual study was done in which treatment B was found to work with higher probability than treatment A, for both large and small kidney stones, despite the fact that treatment A works with higher overall probability than Treatment B. Here's the numbers from the study:
| Treatment A helps | Treatment B helps | |
| Large kidney stones | 69% (55 / 80) | 73% (192 / 263) |
| Small kidney stones | 87% (234 / 270) | 93% (81 / 87) |
| All patients | 83% (289 / 350) | 78% (273 / 350) |
The phenomenon just demonstrated is known as Simpson's paradox. If you're like most people, including me, Simpson's paradox is shocking the first time you meet it. It's got an Alice in Wonderland quality, violating an instinctive way we reason about the world. It's a bit like finding an instance where 1 + 1 somehow turns out to be 3. And, as we'll see through the essay, Simpson's paradox is not a mere curiosity or oddity, it turns up often, and in places that have important decision-making consequences.
As another example of Simpson's paradox, in the 1970s the University of California at Berkeley was sued for discrimination because men were being admitted to graduate school at a higher rate than women. It seemed plausible that discrimination might be involved. However, a close look at the numbers showed that in almost every department women were being admitted at a rate equal to or higher than men. It was Simpson's paradox again.
Simpson's paradox suggests many questions. In the kidney stone example, which treatment should you use, and why? What was really going on at UC Berkeley? What would it take to have convincing evidence of discrimination, or its absence? More fundamentally, why is the reversal going on? While the bare-bones written explanation I've just given states the basic facts of Simpson's paradox, it doesn't help address these other questions. Simpson's paradox shows that some of our ingrained intuitions about statistics are not just wrong, but spectacularly wrong. A really good explanation of Simpson's paradox would help us rebuild our intuition about statistics. The strategy we'll use to develop such an explanation is to identify a series of very specific shortcomings in the bare-bones written explanation. And for each of those shortcomings we'll find a natural way of addressing it using non-traditional media forms -- visualizations, television, and video games.
Reducing the burden on our working memory
A problem with the basic written explanation of Simpson's paradox is that it requires us to keep track of many different relationships between numbers. Explaining those relationships verbally imposes quite a burden on our working memory. Can we represent these numbers visually, in a way that lets us see all the relationships at once in a single picture?
To do this, it turns out to be helpful to use a different example
of Simpson's paradox, one based on voting on the 1964 Civil Rights Act
in the United States House of Representatives. As the following graph
illustrates, in the Northern states 94% of House Democrats voted for
the Civil Rights Act, while in the South just 7% of Democrats voted
for the Civil Rights Act:

Note that I've drawn the North and South results
with overlapping bars. I could have drawn them separately, but it
will turn out that presenting them as overlapping bars makes it easier
to think about the overall fraction of Democrats voting for
the Civil Rights Act.
What is that overall fraction? Before looking at the actual
numbers, let's explore a few possibilities, to get a feel for what's
going on. Suppose for the sake of argument that nearly all Democratic
House Members were from Northern States. Then you'd expect that the
overall fraction of Democrats voting for the Civil Rights Act would be
just a bit less than the fraction in the North:

But suppose instead that
nearly all the Democratic House Members were in the South. Then the
overall fraction voting for the Civil Rights Act would be just a bit
more than the fraction in the South:

In actual fact, the
Democrats were fairly evenly split, with a slight excess (62%) of
Democrats in the North. And so the actual overall fraction of
Democrats voting for the Civil Rights Act is a little above the
midpoint between the Northern and Southern percentages:

Let's switch to look at the Republicans. In the North, 85% of
Republicans voted for the Act, and in the South, 0% of Republicans
voted for it:
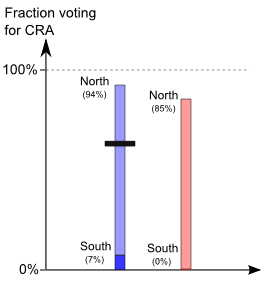
By
comparing the height of the top bars we can see that in the North a
higher fraction of Democrats than Republicans voted for the Civil
Rights Act. By comparing the height of the bottom bars we can see
that the Democrats were also more likely to vote for the Act in the
South.
However, nearly all Republican House members -- 94% of them, in fact
-- came from Northern states. And so the overall fraction of
Republicans voting for the Civil Rights Act was very near the value in
the North:

And so we can see
that overall a greater fraction of Republicans voted for the Civil
Rights Act than did Democrats, despite the fact that in both the North
and South the Democrats were more likely to vote for the Civil Rights
Act. Everything is shown in this one graph: it is, in a sense, a
complete explanation of the facts of Simpson's paradox. And this
visual explanation has the great advantage over the earlier written
explanation that it is much easier to keep track of all the relevant
relationships between different numbers**Not all
visualizations of Simpson's paradox have this property. I have seen
visualizations of the paradox which actually make it harder to
understand, not easier. Visualization is a means, not an end, and
pursuing it for its own sake is a mistake..
Furthermore, we can also see the reason why Simpson's paradox occurred. No matter what their party, Congresspeople from the North were far more likely to vote for the Civil Rights Act than Congresspeople from the South. This difference was much more important than minor party differences within regions. The Democrats had much greater representation in the South than did the Republicans, and this substantially reduced the overall Democrat average, despite the fact that Democrats were more likely to vote for the Act in both North and South. Put another way, what made Simpson's paradox possible is that location mattered far more than party to how people voted.
By the way, this same fact had a big impact on US politics. The Civil Rights Act was passed in 1964. Four years later, the Republican candidate in the 1968 presidential campaign, Richard Nixon, adopted what is now known as the Southern Strategy. That's a euphemistic way of saying that the Republicans began deliberately trying to attract the racist vote in the South -- what one of Nixon's advisors famously called the "Negrophobe" vote. We take this for granted today, but it reversed more than a century of tradition -- the Republicans were, after all, the party of Lincoln. By adopting this strategy, Nixon managed to put many southern states in electoral play which had formerly been Democrat strongholds.
A strength of this explanation is that it makes it easy to visualize
the possible values for the overall Republican vote. We know that for
Simpson's paradox to occur the Republicans have to be concentrated
enough in the North that their overall percentage exceeds the
Democrats' overall percentage:
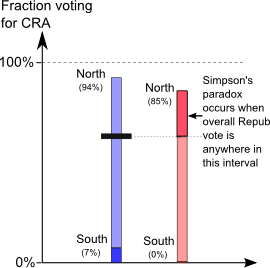
When that happens, the
conditions for Simpson's paradox are met.
Another strength of this explanation is the use of blue bars to represent Democrat votes and red bars to represent Republican votes. Using these standard mnemonic colours further lightens the load on our working memory, and makes it easier to follow the explanation. That's actually why I switched away from the kidney treatment example -- blue for Democrat and red for Republican is more vivid and concrete than the abstract wooliness of "treatment types A and B". Of course, these mnemonics may fail to help if you're colour blind. In that case the use of the colours will have made the explanation harder to follow, not easier.
Changing our habits of mind
While the visual explanation of Simpson's paradox just given has many
strengths, it's still not a great explanation. It makes it easier to
understand the basic facts of Simpson's paradox, but doesn't change
our instinctive intuitive reasoning about probabilities. Suppose in
everyday life someone told you that in both the North and the South,
the Democrats were more likely than the Republicans to vote for the
Civil Rights Act. Unless you'd recently been thinking about Simpson's
paradox, your brain would probably automatically infer that the
Democrats were overall more likely to vote for the Civil Rights
Act:
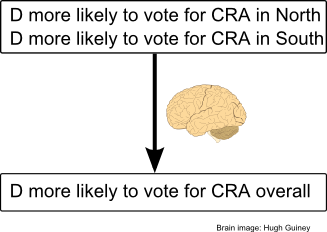
What you want is for your brain to interrupt this automatic
inference. Instead, it should recognize situations of this type, and
understand that alternative explanations are possible:

In particular, and at an
absolute minimum, you should immediately understand that
it is possible the Republicans were more likely, overall, to
vote for the Civil Rights Act than the Democrats.
Of course, while you may know intellectually that this is what you should do, that doesn't mean you'll actually do it when such a situation arises. You can learn everything there is to know about how to swing a tennis racket, but that doesn't mean you'll do the right thing when a tennis ball is bearing down on you on court. Put another way, the core issue here isn't just to learn a set of facts. It's at least as important to replace your old instinctive habits of thought with new habits of thought.
A conventional response to all this is to shrug our shoulders and say that some people are "smart", meaning that they have strategies to convert knowledge of the facts into a change in their habits of thought, and that other people are "not so smart", meaning that they don't apply such strategies. I believe this is wrong, I believe we can and should improve our explanations to help people change their habits of thought.
We can do this by not just providing the facts, but by also directly cueing changes in people's habits of thought. One simple idea for how to do this is to dramatize as vividly as possible the point at which an interruption in our thinking should occur. It's that moment which we want people to recognize and act on, as it occurs.
Most readers have probably seen episodes of the popular 1990s
sitcom Seinfeld. Two of the characters were Kramer,

a slightly seedy character with a quirky intelligence, and George,

the friend no-one wants, always trying to get ahead at the
expense of others, but always failing, mostly because he's not so
bright.
Imagine Kramer and George arguing about which of two baseball players
is better. Kramer thinks
it's Derek
Jeter,

while George
prefers David
Justice,

To settle
which player is better, they make a hundred dollar bet. Kramer wins
if, over the next two seasons, Jeter has a higher batting average than
Justice. George wins if Justice has the higher two-season batting
average.
At the end of the first season, George is happy:

His guy, David
Justice, has done well, and had a higher batting average that season.
Toward the end of the second season, George is tense but
optimistic:

His guy, David Justice, is again ahead in the
averages. The final game comes, it's over, and George is
ecstatic:

His guy has the better season average again!
Now Kramer walks in, quite unconcerned:

George is gloating about his win:

Kramer asks "What
are you so happy about?" George explains: "My guy won, he had the
better average both years. Pay up!"
Then, the punchline. Kramer: "I suppose that's true. But last season
both guys batted great all season. They both had really high
averages, and your guy just beat out my guy. This season both batted
badly. But my guy was out injured almost the whole season. So he
only had a few at-bats, and batting badly only lowered his two-season
average a tiny bit. Your guy batted badly the whole season, and that
lowered his two-season average a lot. So my guy did better overall.
Pay up!"


Of course, Kramer's explanation might whiz by too fast, leaving both the viewer and George unsure exactly what just happened. That'd be in-character for both George and Kramer. You can imagine later scenes in which George complains bitterly to Jerry or Elaine that Kramer must have duped him, and gets really worked up about being fooled like that. And then a final scene in which Kramer goes through it more slowly and in more detail, convincing George (and, incidentally, the viewer) that he really was wrong.
Okay, it's not the best Seinfeld ever. But it does have some good qualities as an explanation.
We've embedded Simpson's paradox in a tense, emotional
situation**There is an extensive
research
literature studying how emotion impacts (and often enhances) our
memory., a situation where we empathize with the characters.
It's no longer a dry, abstract exercise, there's something on the
line. We feel for George when he's wrong, after being so sure that
he's won. After all, even though we don't much like him, we've made
the exact same mistake in our thinking. What's more, the emotional
punch -- the memorable bit -- comes exactly at the moment in which
George is gloating, and Kramer delivers his knockout blow. It's those
few seconds, the few seconds in which George goes from gloating to
crestfallen, which are what we most need to internalize, and they are,
in fact, the most memorable part of the episode. In other words,
what's good about this explanation is that it gives us a concrete
model that vividly demonstrates exactly the failure in thinking that
we should avoid:

Ideally, this will burn
itself into our mind. When we find ourselves in a similar situation,
we'll feel uncomfortable. We'll think: "Isn't this like that episode
of Seinfeld?" Even if we don't remember the details, getting
that discomfort on cue is a huge win in understanding, for it
interrupts our thinking in exactly the way we need to create a new
habit of thought:

Having been
interrupted, what then should we do about that discomfort? A
shortcoming of the Seinfeld explanation is that while it
helps you recognize Simpson's paradox, it doesn't tell you what to do
about it. In particular, it leaves you with no well-articulated
understanding of what to think or how to act when you find yourself in
such a situation. We could improve the explanation by integrating it
with a discussion of Simpson's paradox along the lines of our earlier
visualization. I won't go down the path of figuring out how to do
that, but, done well, the result would be both a vivid model helping
you change your habits of thought, and a (partially, not yet fully)
articulated understanding of Simpson's paradox. That's more powerful
than either alone.
One point demonstrated by the Seinfeld explanation is the value of comedy as a format for vividly modelling counterintuitive ideas. We've made Simpson's paradox a joke. That's possible because Simpson's paradox has the structure of a joke: it has a premise which leads us to expect a particular conclusion, and then BAM, there's a switch and we see that the situation can be understood in a totally different way. It's challenging to get right, though, because the audience may not immediately get the punchline, unless they've been prepared in advance. That requires careful design. The Seinfeld example avoids this pitfall in part by relying on schadenfreude: while we may not get the joke entirely straight away, we get it enough to believe Kramer, and to realize that George is the patsy, yet again. It also helps that I've primed you earlier with a discussion of Simpson's paradox. This perhaps seems like cheating on my part, but comedy writers cheat all the time in just this way, taking pains to set the audience up with just enough information to get the joke.
Raising the emotional stakes
A drawback of the Seinfeld explanation is that it's George, not us, who loses the bet. Instead of watching the dramatization, it'd be better if we personally had money on the line. Imagine, for example, that you are a contestant on a television game show, trying to win a million dollar prize, and winning the prize comes down to understanding Simpson's paradox, just as in George and Kramer's bet. Suppose you get it wrong, and lose the prize. It'd certainly be a great learning experience! At the least you'd become much more cautious about making such errors in the future. In general, we can improve the way we learn by raising the stakes for learning as high as is possible without losing the ability to think calmly about the situation.
Of course, it's difficult to routinely organize such experiences.
There is, however, a natural way of upping the emotional stakes, and
that's to embed Simpson's paradox inside a video game. Suppose you're
in a game where you interact with other characters. One of them
offers a bet:

Ideally, there's a back story here, something connecting you to this
guy, and to both Justice and Jeter. You check the batting averages.
Last season Justice did better. And this season Justice looks to be
doing better again: 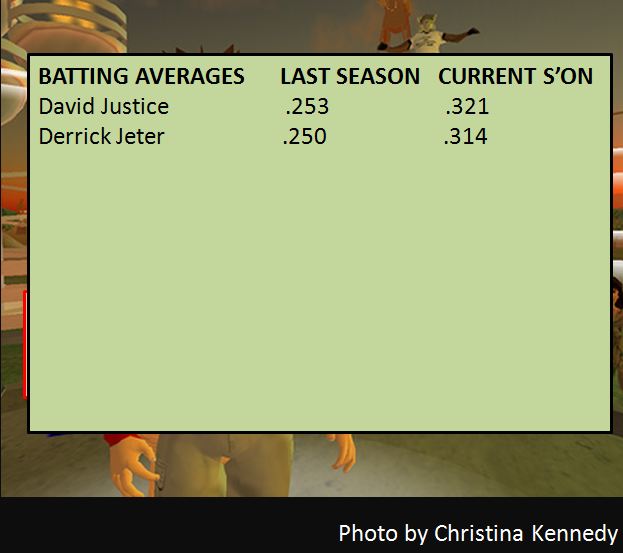
You say "Justice is
better":
They
reply: "No way! Jeter is much better!" and ask you to bet a thousand
dollars that over this season and the previous season, Jeter will have
a better batting average: 
You're suspicious, of course. And your suspicion
is heightened when they tell you they'll give you odds:

But it seems too good
a deal, so you take the bet. Then you see the last game of the
season:

Your guy,
Justice, does well, and he finishes with the higher seasonal batting
average for the second season running. But, of course, it's a setup,
and even though Justice did better in both seasons, Jeter did better
overall:
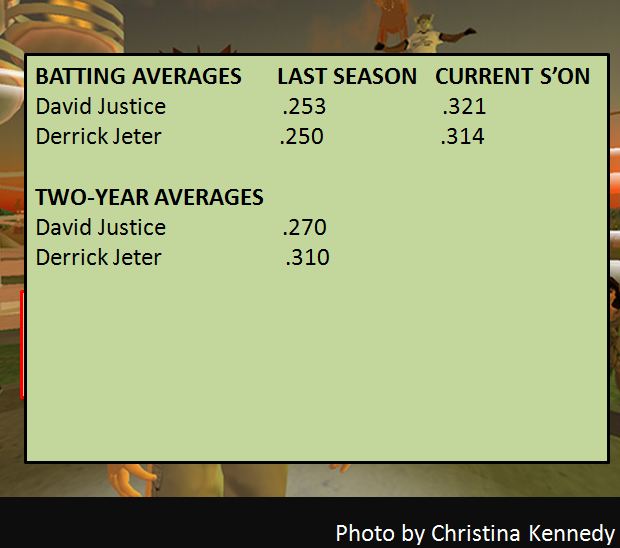
You've
lost your bet! And, again, that moment in which you realize that
you've lost -- the moment where confusion gives way to understanding
and a little embarassment as you realize you've been fooled -- is the
emotionally powerful moment, the moment which imprints on you an
understanding that you'll likely retain.
There's an alternative story in which you're so suspicious of the offered bet that you check everything carefully, and figure out in advance what's going to happen. That's a different kind of learning, but still very useful. Either way, you're directly experiencing Simpson's paradox, and you're personally invested in the outcome.
We can improve this explanation by further upping the stakes of the bet. If the other player is a computer character, the stakes are relatively low. But if the other player is the avatar for a real person, perhaps someone whose good opinion you desire, that ups the stakes considerably. As I said before, we learn most when we have the most to lose.
As an explanation of Simpson's paradox this experience still has
many deficiencies. As in the
Seinfeld explanation, one problem with this explanation is
that the knowledge gained isn't fully articulated. Even if you play
and lose, you don't emerge with an understanding of what precisely to
think or do about Simpson's paradox in future. A way to address that
deficiency is to integrate a designer mode into the game, enabling
players to create new puzzles. Suppose, for instance, that this kind
of bet was one of a class of puzzles you could add to the game. You'd
be presented with a design panel which lets you choose the relevant
settings:

You
can imagine moving around the different parameters, trying to find
settings which guarantee you a win, but which will convince others to
take the bet. And then you inflict the puzzle you've designed on your
friends. The panel could cue you in various ways, helping you
understand why some parameters work and others don't. It'd be a way
of integrating the experience of the bet with a better-articulated
understanding of Simpson's paradox.
You may wonder why I'm paying so much attention to creating emotional involvement? To understand the reason, think about how involved we can get in a great movie or great video game. People may find themselves moved to tears in a great movie, or experience tremendous euphoria after solving a game puzzle. Years later, they may be able to quote lines from a movie scene they saw only once. This strong connection comes because the people who create movies and video games focus on emotional involvement first, and intellectual content second. Viewed from a traditional intellectual point of view, that sounds like a put-down. But what the creators of the movies and games appreciate deeply -- and what many intellectuals do not -- is that emotional involvement is the foundation for understanding. Even when explaining abstract, intellectual subjects -- perhaps, especially when explaining abstract, intellectual subjects -- creating strong emotional involvement is crucial. If someone's desire to understand is strong enough, they can overcome tremendous obstacles. Part of what we can learn from the movie and game makers is how important such desires are, and the art of creating them.
Conclusion
What have we learned by developing this series of prototype explanations? Conventional explanations of Simpson's paradox**For an excellent explanation using a conventional media form, see Judea Pearl's recent essay. provide an abstract verbal and symbolic framework for understanding the paradox. We judge such explanations by the depth and clarity of the framework they develop. By contrast, in my prototypes I've focused on very different goals -- things like emotional impact, changing habits of mind, and reducing the burden on people's short-term working memory. Such goals are often treated as incidental in traditional explanations, but I believe they are just as important as more conventional goals. By changing media forms we've gained access to new patterns of explanation which make it possible to address these new goals in ways difficult or impossible in a traditional verbal explanation. And so I believe it's worth taking non-traditional media seriously not just as a vehicle for popularization or education, which is how they are often viewed, but as an opportunity for explanations which can be, in important ways, deeper.
Of course, we could iterate dozens more times on the prototype explanations that I've described. There's much we still need to address. For example, in the kidney treatment example we never figured out which treatment we should take? How should we understand the UC Berkeley admissions data? Was discrimination going on? A great explanation would leave us with an intuitive understanding for how to answer these questions. There are also many habits of thought related to Simpson's paradox that we need to identify and figure out how to change. For instance, in the Berkeley story we'd like to interrupt the natural intuitive inference that since men have a higher overall admission rate than women, there must be a department-by-department bias. Ideally, we'd find ways of integrating the best ideas from conventional written explanations with the best possibilities afforded by other media. Within a short essay such as this, it's not feasible to do all these things. But it'd be fun to work on.
In fact, what I'd really like to do is work together with a great designer and a great programmer, to explain a subject such as quantum mechanics or quantum computing or quantum field theory**As a small step in this direction I'm considering running a small online discussion group on "Quantum Computing for Designers". Contact me (mn@michaelnielsen.org) if you have a strong background in design and are interested.. I think you could do something truly special. And what I'd really, really like to do is to work on explaining all of physics or all of science in this way. Ideally, you'd have the best designers in the world, and the best explainers in the world, together in a room as equal creative partners, figuring out what is possible.
In the short term, it's tempting to immediately attempt a big project,
like explaining all of science, and to raise money and bring together
a team of designers, artists, programmers, and musicians. Eventually
I'd like to do that, but it's too early. Instead, I plan to explore,
to produce many rough prototypes**One idea I've
long liked is the idea of putting a soundtrack to a scientific talk.
A good movie soundtrack can greatly intensify the experience. Can we
similarly intensify the experience of scientific
explanations?
Another idea is to develop new
representations of fundamental ideas such as probability. In this
essay I represented probabilities using numbers, graphs, and bets.
These are good representations, but I believe we can develop richer,
more concrete representations that would open new possibilities for
explaining ideas such as Simpson's paradox., in collaboration
with a designer or programmer, and to develop a superb vocabulary of
explanation. That'd be a great foundation for a more ambitious
project. Over the long run, humanity will no doubt build the most
powerful new patterns of explanation into our media platforms,
permanently changing and expanding what we mean by explanation. We're
only just beginning to explore these possibilities, but it will be
exciting to see what happens in the decades ahead as we reinvent
explanation.
If you enjoyed this essay, then you may wish to follow me on Twitter or subscribe to my blog.
Comment on this essay on Google Plus
Acknowledgements
This essay is based on a talk given at Idee, makers of reverse image search engine TinEye, and on a talk given at the Santa Fe Institute. Thanks to Leila Boujnane for the invitation to speak at Idee, and for encouraging me to speak about whatever I wanted, and to Cris Moore for inviting me to the Santa Fe Institute. Thanks to Jen Dodd, Ilya Grigorik, and Hassan Masum for many hours (and years) of great conversation about these issues. And thanks to Jen Dodd, Ilya Grigorik, Howard Nielsen, and Rob Spekkens for comments on a draft of the essay.
Addendum on educational games
Something I didn't discuss in the main body of the essay is educational video games, and the vogue for the so-called gamification of learning. Using video games to explain is an old idea, going back to the 1960s, and the subject obviously overlaps with the theme of my essay. To properly discuss the relationship really needs an entire essay of its own; I will restrict myself here to a few brief remarks.
One problem with educational games lies in the word "games". Video game companies have created an extremely successful business model which aligns very well with the goal of providing entertainment, and somewhat less well with the goal of providing great explanations. Inevitably, the business model sometimes conflicts with the goal of great explanation. When that happens it is not surprising that the game companies prioritize their business, at the expense of the quality of explanation. To put it another way, when the goal of explanation comes in conflict with the goal of creating a good game, the more successful game companies go with creating a good game.
A second problem with educational games lies in the word "educational". The most important fact about compulsory schooling is that students do not -- indeed, cannot -- choose to attend. Instead, they are required to attend, for what society deems "their own good". This is true even in the most enlightened schools. A student in such a coercive environment does not have full responsibility for their own learning. And, in my opinion, it is not possible to do serious intellectual work without full responsibility for your own learning. Put another way, I believe that compulsory schools, by their nature, are places where serious intellectual work cannot occur.
Many people will no doubt strongly disagree with the points in one or both of the last two paragraphs. The paragraphs are not meant to convince skeptics -- that would take an extended essay, at the very least -- but are merely a statement of what I believe. Of course, in practice my thinking has been deeply influenced by people working in education, and by people from the gaming industry. However, I believe there is value in sometimes entirely setting aside the "educational games" framing, and instead approaching the problem of explanation from first principles. That's the spirit in which I've written the current essay, and why I have not directly engaged the subject of educational games in the main text of the essay.
Addendum on motivation
What follows is my first attempt at drafting an opening to this essay. I eventually abandoned this opening, since it doesn't quite fit with the rest of the essay. I've included it (slightly abridged) as an addendum since the material is important to me personally, and may perhaps connect to some readers.
In September 2013 the video game company Rockstar Games released the game Grand Theft Auto V. The game made headlines, taking in a staggering 800 million dollars in its first day of sales. But equally remarkable, though less headline-inducing, the game cost a quarter billion dollars to create.
Inspired by Grand Theft Auto, the question motivating this essay is: what would happen if we put the resources and talent of a major video game or movie studio toward creating great explanations, rather than pure entertainment products? What could Rockstar Games achieve if they spent even a tiny fraction of that quarter billion dollars creating, say, a digital reimagining of the physicist Richard Feynman's famous Feynman Lectures on Physics? Or what happens if a movie director such as James Cameron, the creator of movies such as Avatar and Titanic, turns his resources toward reinventing a classic such as Molecular Biology of the Cell?
Such questions are interesting because the big video game and movie studios employ armies of talented designers, programmers, artists, animators, and musicians. Whether you like Grand Theft Auto or not, it's an extraordinary caricature of the sleazy side of Los Angeles. What happens when you marry the talent behind it and similar games to the incredible insight and explanatory ability of Richard Feynman or another of our great explainers, someone like E. O. Wilson, or Steven Pinker, or Richard Dawkins?
To be clear, I'm not talking about doing something silly like literally converting The Feynman Lectures into a game format. Instead, I'm talking about thinking very hard about how to explain when you're not using paper and print, but rather bits and microprocessors. We do not yet understand the answer to that question. I believe our current efforts with digital explanation are analogous to the efforts of the early silent film-makers, or to painters prior to the Florentine Renaissance. We haven't yet found our Michaelangelo and Leonardo, we don't yet know what is possible in this medium. In fact, we don't yet have even the basic vocabulary of digital explanation.
What we do have is a small cadre of people doing wonderful prototype work developing that vocabulary of explanation -- people such as Bret Victor, Vi Hart, Chaim Gingold, Jonathan Blow, and others.
For my own part, what I'd like to do is help create media which make it possible for a teenager to understand quantum mechanics, say, as well as or better than a professor of physics does today. Or to understand the cell as well as or better than a professor of biology does today. Conventional wisdom says that only a tiny fraction of the population, perhaps one percent, has the talent for physics or biology needed to fall in love with these subjects, and then to put in the effort needed to master them. I believe the conventional wisdom is wrong, I believe we can create vastly better digital explanations, explanations which will help far more people connect with these subjects, fall in love with them, and achieve mastery. How can we achieve this?