This is the title of a thought-provoking essay by Tim Gowers, which seems to have been stimulated in part by my recent essay on doing science online. What follows are some excerpts from Gowers’ essay, and some thoughts by me:
Of course, one might say, there are certain kinds of problems that lend themselves to huge collaborations. One has only to think of the proof of the classification of finite simple groups, or of a rather different kind of example such as a search for a new largest prime carried out during the downtime of thousands of PCs around the world. But my question is a different one. What about the solving of a problem that does not naturally split up into a vast number of subtasks? Are such problems best tackled by n people for some n that belongs to the set \{1,2,3\}? (Examples of famous papers with four authors do not count as an interesting answer to this question.)
It seems to me that, at least in theory, a different model could work: different, that is, from the usual model of people working in isolation or collaborating with one or two others. Suppose one had a forum (in the non-technical sense, but quite possibly in the technical sense as well) for the online discussion of a particular problem. The idea would be that anybody who had anything whatsoever to say about the problem could chip in. And the ethos of the forum — in whatever form it took — would be that comments would mostly be kept short. In other words, what you would not tend to do, at least if you wanted to keep within the spirit of things, is spend a month thinking hard about the problem and then come back and write ten pages about it. Rather, you would contribute ideas even if they were undeveloped and/or likely to be wrong.
A similar approach is used in the open-source software community – essentially, a dynamic division of labour that is not planned entirely in advance, but rather arises in response to the exigencies of the problem at hand. This dynamic division of labour is typically co-ordinated through one or more online forums. Examples close to this spirit, and also somewhat close in spirit to modern mathematics include Kasparov versus the World and the Matlab programming competition.
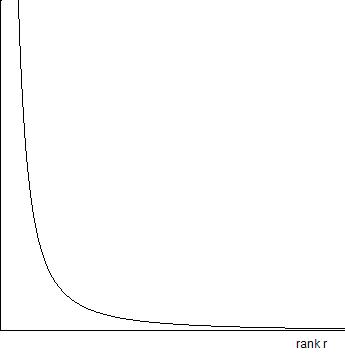
On the subject of the desirable size of contributions, in open source the most frequent contributions change just a single line of code. The second most frequent contributions change two lines of code, and so on. One study suggests the number of contributions [tex]n[/tex] scales as [tex]n(l) \propto l^{-1.13}[/tex], where [tex]l[/tex] is the number of lines of code changed or added (“committed”) in a single contribution.
It’s notable that with this distribution the total line count is still dominated by the larger contributions. Despite this, my guess is that the smaller contributions are still very significant for maintaining momentum and morale, which are so important in creative projects. In this regard, it’s a little like a good creative conversation – not all contributions to the conversation need to be world-shaking, some are simply needed to keep the conversation moving.
This suggestion raises several questions immediately. First of all, what would be the advantage of proceeding in this way? My answer is that I don’t know for sure that there would be an advantage. However, I can see the following potential advantages.
(i) Sometimes luck is needed to have the idea that solves a problem. If lots of people think about a problem, then just on probabilistic grounds there is more chance that one of them will have that bit of luck.
(ii) Furthermore, we don’t have to confine ourselves to a purely probabilistic argument: different people know different things, so the knowledge that a large group can bring to bear on a problem is significantly greater than the knowledge that one or two individuals will have. This is not just knowledge of different areas of mathematics, but also the rather harder to describe knowledge of particular little tricks that work well for certain types of subproblem, or the kind of expertise that might enable someone to say, “That idea that you thought was a bit speculative is rather similar to a technique used to solve such-and-such a problem, so it might well have a chance of working,” or “The lemma you suggested trying to prove is known to be false,” and so on—the type of thing that one can take weeks or months to discover if one is working on one’s own.
I think of this as the “annoying little conjecture” problem: many conjectures that arise in the course of research are often essentially routine to prove or disprove, but it can take days or weeks to determine which it’s going to be. If you talk to just the right person, they can often cut that down to minutes or hours. Ordinarily, though, finding that right person is often just as laborious (and may be less enlightening) than solvig the problem yourself. Having a mechanism to find the right person, even if it’s essentially just broadcast search, would be enormously beneficial.
The next obvious question is this. Why would anyone agree to share their ideas? Surely we work on problems in order to be able to publish solutions and get credit for them. And what if the big collaboration resulted in a very good idea? Isn’t there a danger that somebody would manage to use the idea to solve the problem and rush to (individual) publication?
Here is where the beauty of blogs, wikis, forums etc. comes in: they are completely public, as is their entire history. To see what effect this might have, imagine that a problem was being solved via comments on a blog post. Suppose that the blog was pretty active and that the post was getting several interesting comments. And suppose that you had an idea that you thought might be a good one. Instead of the usual reaction of being afraid to share it in case someone else beat you to the solution, you would be afraid not to share it in case someone beat you to that particular idea. And if the problem eventually got solved, and published under some pseudonym like Polymath, say, with a footnote linking to the blog and explaining how the problem had been solved, then anybody could go to the blog and look at all the comments. And there they would find your idea and would know precisely what you had contributed. There might be arguments about which ideas had proved to be most important to the solution, but at least all the evidence would be there for everybody to look at.
The open source world demonstrates this in action. You can see every single contribution a person has made to a project – the code, the conversations in online forums, and so on. There’s even beautiful visualizations that let you see different people’s contributions to a project. As a result, it’s very difficult to fool people about the extent of your contributions. I’m sure people are sometimes dishonest about this, but I’ll bet they’re a lot more honest than some scientists are about what they contributed to some papers.
True, it might be quite hard to say on your CV, “I had an idea that proved essential to Polymath’s solution of the *** problem,” but if you made significant contributions to several collaborative projects of this kind, then you might well start to earn a reputation amongst people who read mathematical blogs, and that is likely to count for something. (Even if it doesn’t count for all that much now, it is likely to become increasingly important.) And it might not be as hard as all that to put it on your CV: you could think of yourself as a joint author, with the added advantage that people could find out exactly what you had contributed.
And what about the person who tries to cut and run when the project is 85 [percent] finished? Well, it might happen, but everyone would know that they had done it. The referee of the paper would, one hopes, say, “Erm, should you not credit Polymath for your crucial Lemma 13?” And that would be rather an embarrassing thing to have to do.
Now I don’t believe that this approach to problem solving is likely to be good for everything. For example, it seems highly unlikely that one could persuade lots of people to share good ideas about the Riemann hypothesis.
At present, this is undoubtedly true. However, if this sort of approach takes off and comes to be seen as a legitimate and orthodox way of making a contribution to mathematics, the kind of thing valued by (for example) hiring committees, then I think it may eventually be possible to do this for some of the more famous problems. There’s no intrinsic difference between sharing your ideas in a paper, or in a blog comment: a good idea is a good idea. The difference at present is mainly social: one is seen as legitimate, while the other is questionable.
At the other end of the scale, it seems unlikely that anybody would bother to contribute to the solution of a very minor and specialized problem. Nevertheless, I think there is a middle ground that might well be worth exploring, so as an experiment I am going to suggest a problem and see what happens.
I think it is important to do more than just say what the problem is. In order to try to get something started, I shall describe a very preliminary idea I once had for solving a problem that interests me (and several other people) greatly, but that isn’t the holy grail of my area. Like many mathematical ideas, mine runs up against a brick wall fairly quickly. However, like many brick walls, this one doesn’t quite prove that the approach is completely hopeless—just that it definitely needs a new idea.
It may be that somebody will almost instantly be able to persuade me that the idea is completely hopeless. But that would be great—I could stop thinking about it. And if that happens I’ll dig out another idea for a different problem and try that instead.
I’ve been toying for quite some time with doing something similar, though with problems from theoretical physics. I’ll be utterly fascinated to see the result of this experiment, and will certainly follow along. Not sure I’ll have much of mathematical interest to contribute, though – combinatorics is a long way from my expertise.
It’s probably best to keep this post separate from the actual mathematics, so that comments about collaborative problem-solving in general don’t get mixed up with mathematical thoughts about the particular problem I have in mind. So I’ll describe the project in my next post. Actually, make that my next post but one. The next post will say what the problem is and give enough background information about it to make it possible for anybody with a modest knowledge of combinatorics (or more than a modest knowledge) to think about it and understand my preliminary idea. The following post will explain what that preliminary idea is, and where it runs into difficulties. Then it will be over to you, or rather over to us. I’ve already written the background-information post, but will hold it back for a few days in case the responses to this post affect how I decide to do things.
The blog medium is almost certainly not optimal for this purpose, so if a serious discussion starts with lots of worthwhile contributions, then I’ll look into the possibility of migrating it over to some purpose-built site. If anyone has any suggestions for this (apart from the obvious one of using the Tricki — I’m not sure that’s appropriate just yet though) then I’d be delighted to receive them. My feelings at the moment are that blogs are too linear—it would be quite hard to see which comments relate to which, which ones are most worth reading, and so on. A wiki, on the other hand, seems not to be linear enough—it would be quite hard to see what order the comments come in. So my guess is that the ideal forum would probably be a forum: if someone knows an easy way to set up a mathematical forum, I might even do that. But if the discussion is on this blog, then I might from time to time try to assess where it has got to and create new posts if I feel that genuine progress has been made that can be summarized and then built on.
I’ve been thinking of doing this for a long time. The reason I’ve suddenly decided to go ahead is that I followed a couple of links from this post on Michael Nielsen’s blog, and discovered that, unsurprisingly, others have had similar ideas, and some people are already doing research in public. But the idea still seems pretty new, particularly when applied to one single mathematics problem, so I wanted to try it out when it was still fresh. (I would distinguish what I am proposing from what goes on at the n-category café, which is an excellent example of collaborative mathematics, but focused on an entire research programme rather than just one problem.)
To finish, here is a set of ground rules that I hope it will be possible to abide by. At this stage I’m just guessing what will work, so these rules are subject to change. If you can see obvious flaws let me know.
1. The aim will be to produce a proof in a top-down manner. Thus, at least to start with, comments should be short and not too technical: they would be more like feasibility studies of various ideas.
2. Comments should be as easy to understand as is humanly possible. For a truly collaborative project it is not enough to have a good idea: you have to express it in such a way that others can build on it.
Points 3-5 all concern norms of behaviour, and the problem of maintaining a civil tone:
3. When you do research, you are more likely to succeed if you try out lots of stupid ideas. Similarly, stupid comments are welcome here. (In the sense in which I am using “stupid”, it means something completely different from “unintelligent”. It just means not fully thought through.)
4. If you can see why somebody else’s comment is stupid, point it out in a polite way. And if someone points out that your comment is stupid, do not take offence: better to have had five stupid ideas than no ideas at all. And if somebody wrongly points out that your idea is stupid, it is even more important not to take offence: just explain gently why their dismissal of your idea is itself stupid.
5. Don’t actually use the word “stupid”, except perhaps of yourself.
Clay Shirky has pointed out that this problem – the problem of maintaining healthy conduct in online communities – has been around for decades, yet because no-one has synthesized all that is known, the same mistakes keep being made over and over (and over and over) again. The closest thing I know is a short blog post(!) from Theresa Nielsen Hayden, which is nice, but hardly comprehensive. Two suggestions:
- Don’t allow anonymous posting. Forums which do seem inevitably to degenerate. At the least, people should use a consistent handle, and ideally they should be strongly encouraged to use their real name.
- People who want the forum to thrive need to take ownership of social problems. If someone is behaving inappropriately, they should step up to the plate, and gently (at first) suggest alternate conduct. If someone’s behaving like an ass at a dinner party, you don’t leave it all on the host’s shoulders; you try to help out yourself, in whatever ways seem appropriate.
6. The ideal outcome would be a solution of the problem with no single individual having to think all that hard. The hard thought would be done by a sort of super-mathematician whose brain is distributed amongst bits of the brains of lots of interlinked people. So try to resist the temptation to go away and think about something and come back with carefully polished thoughts: just give quick reactions to what you read and hope that the conversation will develop in good directions.
At a talk last year by Mike Beltzner (who manages the development of the front-end for Firefox), he made a case that open-source projects where people went away and coded a lot on their own, only occasionally coming back to add big polished chunks, almost invariably failed.
7. If you are convinced that you could answer a question, but it would just need a couple of weeks to go away and try a few things out, then still resist the temptation to do that. Instead, explain briefly, but as precisely as you can, why you think it is feasible to answer the question and see if the collective approach gets to the answer more quickly. (The hope is that every big idea can be broken down into a sequence of small ideas. The job of any individual collaborator is to have these small ideas until the big idea becomes obvious — and therefore just a small addition to what has gone before.) Only go off on your own if there is a general consensus that that is what you should do.
8. Similarly, suppose that somebody has an imprecise idea and you think that you can write out a fully precise version. This could be extremely valuable to the project, but don’t rush ahead and do it. First, announce in a comment what you think you can do. If the responses to your comment suggest that others would welcome a fully detailed proof of some substatement, then write a further comment with a fully motivated explanation of what it is you can prove, and give a link to a pdf file that contains the proof.
9. Actual technical work, as described in 8, will mainly be of use if it can be treated as a module. That is, one would ideally like the result to be a short statement that others can use without understanding its proof.
If the project thrives, a wiki may be a good place to keep reference materials like this. It seems to be a pretty common pattern for big online collaborations to use a discussion forum to manage the basic conversation, and a wiki for reference materials. Initially, a wiki might not be necessary, and probably shouldn’t be added until there is real demand.
Some wiki software that seems pretty good for mathematical use is the instiki and the TiddlyWiki. Instiki is very well suited for mathematical use; TiddlyWiki wasn’t so much designed for that purpose, but as you can see here seems to work pretty well in practice.
10. Keep the discussion focused. For instance, if the project concerns a particular approach to a particular problem (as it will do at first), and it causes you to think of a completely different approach to that problem, or of a possible way of solving a different problem, then by all means mention this, but don’t disappear down a different track.
11. However, if the different track seems to be particularly fruitful, then it would perhaps be OK to suggest it, and if there is widespread agreement that it would in fact be a good idea to abandon the original project (possibly temporarily) and pursue a new one — a kind of decision that individual mathematicians make all the time — then that is permissible.
I’m not sure what I think about this. It seems rather constraining – why not do some preliminary exploration of the alternate track, if it seems promising? I agree that it would be problematic if it distracted other people too much, but that seems like a problem that could be dealt with, probably in real time, if it comes up.
12. Suppose the experiment actually results in something publishable. Even if only a very small number of people contribute the lion’s share of the ideas, the paper will still be submitted under a collective pseudonym with a link to the entire online discussion.
A couple of final comments.
First, in many ways this (like most open source projects) seems to be primarily a community-building project. If you look at a successful open source-style project – Wikipedia, Linux, the Matlab competition, Kasparov versus the World – at the centre there is always a person who spends a great deal of time simply building and maintaining a healthy community of contributors. I can’t imagine this will be any different.
Second, the systems used need to be easily integrable into people’s workflow. I like the idea of starting on the blog, simply because many people are already in the habit of checking blogs. Migrations to other platforms will need to be handled carefully, to ensure that everyone does start using the new platform successfully. Providing things like RSS feeds or email update services might help greatly with this.