This is one in a series of posts about the Google Technology Stack – PageRank, MapReduce, and so on – based on a lecture series I’m giving in 2008 and 2009. If you’d like to know more about the series, please see the course syllabus. There is a FriendFeed room for the series here.
In today’s lecture, we’ll build our intuition about PageRank. We’ll figure out the minimal and maximal possible values for PageRank; study how PageRank works for a web with a random link structure, seeing a sort of “central limit theorem” for PageRank emerge; and find out how spammers can spam PageRank, and how to defeat them.
Building our PageRank Intuition
In the last lecture we defined PageRank, but we haven’t yet developed a deep understanding. In this lecture we’ll build our intuition, working through many basic examples of PageRank in action, and answering many fundamental questions.
The minimal and maximal values for PageRank
Recall from last lecture that the PageRank vector [tex]q[/tex] is an [tex]N[/tex]-dimensional probability distribution, with the probability [tex]q_j[/tex] measuring the importance of webpage [tex]j[/tex]. Because [tex]q[/tex] is a probability distribution, the total of all the probabilities must add up to one, and so the average PageRank is [tex]1/N[/tex].
It’s interesting that we can get this precise value for the average PageRank, but what we’d really like is more detailed information about the way PageRank behaves for typical pages. Let’s start by studying the minimal and maximal possible values for PageRank.
Intuitively, we expect that the minimal value for PageRank occurs when a page isn’t linked to by any other page. This intuition can be made more rigorous as follows. Recall our definition of PageRank using a websurfer randomly surfing through webpages. At any given step of their random walk, the crazy websurfer has a probability at least [tex]t P_j[/tex] of teleporting to vertex [tex]j[/tex], and thus we must have
[tex] q_j \geq t P_j [/tex]
for all pages [tex]j[/tex]. Furthermore, it’s possible for the PageRank to be equal to this value if, for example, no other pages link to page [tex]j[/tex]. Thus [tex]tP_j[/tex] is the minimal value for the PageRank of page [tex]j[/tex]. A more algebraic way of putting this argument is to recall from the last lecture that [tex]tP = (I-sG)q[/tex], and thus [tex]t P_j = q_j – s(Gq)_j \leq q_j[/tex], since [tex](Gq)_j \geq 0[/tex]. For the original PageRank algorithm, [tex]P_j = 1/N[/tex], and so the minimal PageRank is [tex]t/N[/tex] for all webpages, a factor [tex]t[/tex] smaller than the average PageRank.
Exercises
- We will say that webpage [tex]k[/tex] eventually leads to webpage [tex]j[/tex] if there is a link path leading from [tex]k[/tex] to [tex]j[/tex]. Show that [tex]q_j = tP_j[/tex] if and only if [tex]P_k = 0[/tex] for all pages [tex]k[/tex] that eventually lead to page [tex]j[/tex]. Obviously, this can’t happen for the original PageRank algorithm, where [tex]P_j = 1/N[/tex], unless there are no pages at all linking to page [tex]j[/tex]. Generically, therefore, most pages have PageRank greater than this minimum.
We can use the value for the minimal PageRank to deduce the maximal possible PageRank. Because the sum of all PageRanks is [tex]1[/tex], the maximal possible PageRank for page [tex]j[/tex] occurs if all other PageRanks have their minimal value, [tex]tP_k[/tex]. In this case [tex]q_j = 1-\sum_{k\neq j} t P_k = 1-t(1-P_j) = s+tP_j[/tex], and so we have
[tex] q_j \leq s + t P_j. [/tex]
An example where maximal PageRank occurs is a web with a “star” topology of links, with the central webpage, which we’ll label [tex]1[/tex], having only a single outgoing link, to itself, and every other webpage [tex]2,\ldots,N[/tex] having a single link going to page [tex]1[/tex]. Pages [tex]2,\ldots,N[/tex] have no incoming links, and thus have minimal PageRank [tex]tP_j[/tex], and so page [tex]1[/tex] has maximal PageRank, [tex]s+tP_1[/tex].
Exercises
- In the previous example show explicitly that [tex]q = (s+tP_1,tP_2,\ldots,tP_N)[/tex] satisfies the equation [tex]Mq = q[/tex].
- In the star topology example, we required that webpage [tex]1[/tex] link to itself. The reason was so that page [tex]1[/tex] was not a dangling page, and thus treated by PageRank as effectively linked to every page. What happens to the PageRank of page [tex]1[/tex] if we make it dangling?
Typical values of PageRank
It’s all very well to know the maximal and minimal values of PageRank, but in practice those situations are rather unusual. What can we say about typical values of PageRank? To answer this question, let’s build a model of the web, and study its properties. We’ll assume a very simple model of a web with just 5,000 pages, with each page randomly linking to 10 others. The following code plots a histogram of the PageRanks, for the case [tex]s = 0.85[/tex].
# Generates a 5,000 page web, with each page randomly
# linked to 10 others, computes the PageRank vector, and
# plots a histogram of PageRanks.
#
# Runs under python 2.5 with the numpy and matplotlib
# libraries. If these are not already installed, you'll
# need to install them.
from numpy import *
import random
import matplotlib.pyplot as plt
# Returns an n-dimensional column vector with m random
# entries set to 1. There must be a more elegant way to
# do this!
def randomcolumn(n,m):
values = random.sample(range(0,n-1),m)
rc = mat(zeros((n,1)))
for value in values:
rc[value,0] = 1
return rc
# Returns the G matrix for an n-webpage web where every
# page is linked to m other pages.
def randomG(n,m):
G = mat(zeros((n,n)))
for j in range(0,n-1):
G[:,j] = randomcolumn(n,m)
return (1.0/m)*G
# Returns the PageRank vector for a web with parameter s
# and whose link structure is described by the matrix G.
def pagerank(G,s):
n = G.shape[0]
id = mat(eye(n))
teleport = mat(ones((n,1)))/n
return (1-s)*((id-s*G).I)*teleport
G = randomG(5000,20)
pr = pagerank(G,0.85)
print std(pr)
plt.hist(pr,50)
plt.show()
Problems
- The randomcolumn function in the code above isn’t very elegant. Can you find a better way of implementing it?
The result of running the code is the following histogram of PageRank values – the horizontal axis is PageRank, while the vertical axis is the frequency with which it occurs:
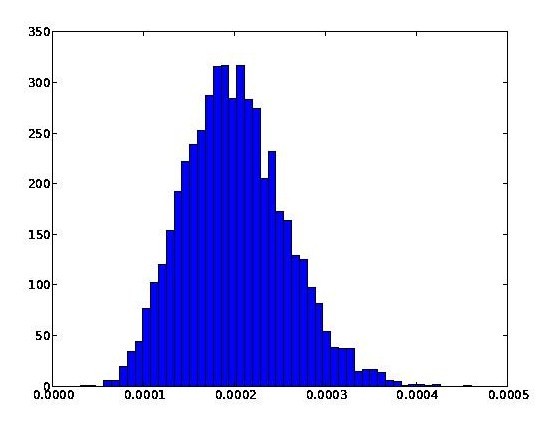
We see from this graph that PageRank has a mean of [tex]1/5000[/tex], as we expect, and an empirical standard deviation of [tex]0.000055[/tex]. Roughly speaking, it looks Gaussian, although, of course, PageRank is bounded above and below, and so can’t literally be Gaussian.
Suppose now that we change the number of links per page to [tex]100[/tex], but keep everything else the same. Then the resulting histogram is:
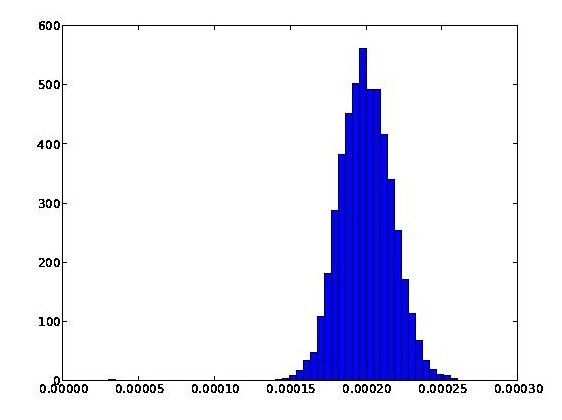
This also looks Gaussian, but has a smaller standard deviation of [tex]0.000017[/tex]. Notice that while we approach the minimal possible value of PageRank ([tex]t/N = 0.00003[/tex]) in the first graph, in neither graph do we come anywhere near the maximal possible value of PageRank, which is just a tad over [tex]s = 0.85[/tex].
Looking at these results, and running more numerical experiments in a similar vein, we see that as the number of outgoing links is increased, the standard deviation in PageRank seems to decrease. A bit of playing around suggests that the standard deviation decreases as one over the square root of the number of outgoing links, at least when the number of outgoing links is small compared with the total number of pages. More numerical experimentation suggests that the standard deviation is also proportional to [tex]s/N[/tex]. As a result, I conjecture:
Conjecture: Consider a random web with [tex]n[/tex] pages and [tex]m[/tex] outgoing links per page. Then for [tex]1 \ll m \ll n[/tex] the PageRank distribution approaches a Gaussian with mean [tex]1/n[/tex] and standard deviation [tex]s/(n\sqrt{m})[/tex].
For the case [tex]n = 5000, m = 10, s = 0.85[/tex] this suggests a standard deviation of [tex]0.000054[/tex], while for the case [tex]n = 5000, m = 100, s = 0.85[/tex] it suggests a standard deviation of [tex]0.000017[/tex]. Both these results are in close accord with the earlier empirical findings. The further numerical investigations I’ve done (not a lot, it must be said) also confirm it.
Incidentally, you might wonder why I chose to use a web containing [tex]5,000[/tex] pages. The way I’ve computed PageRank in the program above, we compute the matrix inverse of a [tex]5,000[/tex] by [tex]5,000[/tex] matrix. Assuming we’re using [tex]64[/tex]-bit floating point arithmetic, that means just storing the matrix requires [tex]200[/tex] megabytes. Not surprisingly, it turns out that my small laptop can’t cope with [tex]10,000[/tex] webpages, so I stuck with [tex]5,000[/tex]. Still, it’s notable that at that size the program still ran quite quickly. In the next lecture we’ll see how to cope with much larger sets of webpages.
Exercises
- Modify the program above to run with [tex]m=1[/tex]. You’ll find that the PageRank distribution does not look Gaussian. What conjecture do you think describes the PageRank distribution in this case? What’s a good reason we might not expect Gaussian behaviour for small values of [tex]m[/tex]?
- Do you trust the Python code to produce the correct outcomes? One of the problems in using numeric libraries as black boxes is that it can be hard to distinguish between real results and numerical artifacts. How would you determine which is the case for the code above? (For the record, I do believe the results, but have plans to do more checks in later lectures!)
Problems
- Can you prove or disprove the above conjecture? If it’s wrong, is there another similar type of result you can prove for PageRank, a sort of “central limit theorem” for PageRank? Certainly, the empirical results strongly suggest that some type of result in this vein is true! I expect that a good strategy for attacking this problem is to first think about the problem from first principles, and, if you’re getting stuck, to consult some of the literature about random walks on random graphs.
- What happens if instead of linking to a fixed number of webpages, the random link structure is governed by a probability distribution? You might like to do some computational experiments, and perhaps formulate (and, ideally, prove) a conjecture for this case.
- Following up on the last problem, I believe that a much better model of the web than the one we’ve used is to assume a power-law distribution of incoming (not outgoing) links to every page. Can you formulate (and, ideally, prove) a type of central limit theorem for PageRank in this case? I expect to see a much broader distribution of PageRanks than the Gaussian we saw in the case of a fixed number of outgoing links.
A simple technique to spam PageRank
One of the difficulties faced by search engines is spammers who try to artificially inflate the prominence of webpages by pumping up their PageRank. To defeat this problem, we need to understand how such inflation can be done, and find ways of avoiding it. Here’s one simple technique for getting a high PageRank.
Suppose the web contains [tex]N[/tex] pages, and we build a link farm containing [tex]M[/tex] additional pages, in the star topology described earlier. That is, we number our link farm pages [tex]1,\ldots,M[/tex], make page [tex]1[/tex] link only to itself, and all the other pages link only to page [tex]1[/tex]. Then if we use the original PageRank, with uniform teleportation probabilities [tex]1/(N+M)[/tex], a similar argument to earlier shows that the PageRank for page [tex]1[/tex] is
[tex] (s + t/M) \frac{M}{M+N}. [/tex]
As we increase the size, [tex]M[/tex], of the link farm it eventually becomes comparable to the size of the rest of the web, [tex]N[/tex], and this results in an enormous PageRank for page [tex]1[/tex] of the link farm. This is not just a theoretical scenario. In the past, spammers have built link farms containing billions of pages, using a technique similar to that described above to inflate their PageRank. They can then sell links from page 1 to other pages on the web, essentially renting out some of their PageRank.
How could we defeat this strategy? If we assume that we can detect the link farm being built, then a straightforward way of dealing with it is to modify the teleportation vector so that all pages in the link farm are assigned teleportation probabilities of zero, eliminating all the spurious PageRank accumulated due to the large number of pages in the link farm. Unfortunately, this still leaves the problem of detecting the link farm to begin with. That’s not so easy, and I won’t discuss it in this lecture, although I hope to come back to it in a later lecture.
Exercises
- Prove that the PageRank for page [tex]1[/tex] of the link farm is, as claimed above, [tex](s+t/M) M/(M+N)[/tex].
- The link topology described for the link farm is not very realistic. To get all the pages into the Google index the link farm would need to be crawled by Google’s webcrawler. But the crawler would never discover most of the pages, since they aren’t linked to by any other pages. Can you think of a more easily discoverable link farm topology that still gains at least one of the pages a large PageRank?
That concludes the second lecture. Next lecture, we’ll look at how to build a more serious implementation of PageRank, one that can be applied to a web containing millions of pages, not just thousands of pages.

