Today I get back into my post series about the Google Technology Stack, with a more detailed look at distributed dictionaries, AKA distributed key-value stores, AKA distributed hash tables. What we’d like to do is store a dictionary of key-value pairs [tex](k_1,v_1),(k_2,v_2),\ldots[/tex] across a cluster of computers, preferably in a way that makes it easy to manipulate the dictionary without having to think about the details of the cluster.
The reason we’re interested in distributed dictionaries is because they’re used as input and output to the MapReduce framework for distributed computing. Of course, that’s not the only reason distributed dictionaries are interesting – they’re useful for many other purposes (e.g., distributed caching). But for the purposes of this post, we’ll imagine our distributed dictionaries are being used as the input and output from a MapReduce job.
I’ll describe two ways of implementing distributed dictionaries. The first is a naive method that’s simple and works pretty well. Then I’ll introduce an improved method called “consistent hashing”. Consistent hashing isn’t the final word in distributed dictionaries, but it’s a good start. All the usual caveats apply to the post: I’m still learning this stuff, and corrections, improvements, etcetera are welcome!
Let’s start with the naive method. Suppose we have a cluster of [tex]n[/tex] computers. We number the computers [tex]0,1,2,\ldots,n-1[/tex], and then store the key-value pair [tex](k,v)[/tex] on computer number [tex]\mbox{hash}(k) \mod n[/tex], where [tex]\mbox{hash}(\cdot)[/tex] is a hash function. If we’re using a good hash function, then [tex]\mbox{hash}(k) \mod n[/tex] is uniform across [tex]0,\ldots,n-1[/tex] for any reasonable distribution of keys. This ensures our distributed dictionary is spread evenly across the computers in our cluster, and doesn’t build up too much on any individual computer.
As a brief Pythonic aside, Python’s builtin hash function doesn’t have this property of spreading keys out uniformly. It sometimes takes similar key strings to similar hash values. Here’s a typical sample (results may vary on your machine):
hash("answer0") -> 1291065813204512909
hash("answer1") -> 1291065813204512908
hash("answer2") -> 1291065813204512911
What this means is that you can’t depend on Python’s builtin hash function to spread keys and values uniformly across the cluster. In principle, far better hash functions are available through the hashlib library, functions which do offer guarantees about uniformity. Those functions are quite a lot slower than hash – I did a little benchmark comparing hash to the hashlib.md5 hash, and found that hash was about ten times faster. We’ll use the hashlib library, although in practice I imagine you’d want something faster, but without the disadvantages of hash. End of Pythonic aside.
Naive hash-based distributed dictionaries are simple, but they have serious limitations. Imagine you’re using a cluster of computers to crawl the web. You store the results of your crawl in a distributed dictionary. But as the size of the crawl grows, you’ll want to add machines to your cluster. Suppose you add even just a single machine. Instead of computing [tex]\mbox{hash}((k) \mod n[/tex] we’re now computing [tex]\mbox{hash}(k) \mod (n+1)[/tex]. The result is that each key-value pair will get reallocated completely at random across the cluster. You’ll end up moving a fraction [tex]n/(n+1)[/tex] of your data to new machines – i.e., nearly all of it. This will be slow, and might potentially be expensive. It’s also potentially inconvenient if jobs are being carried out. Similar problems arise if you add a larger block of machines to the cluster, or if you lose some machines (e.g., if some of the machines fail). You get the idea.
Consistent hashing solves these problems. Like naive hashing, consistent hashing spreads the distributed dictionary evenly across the cluster. But unlike naive hashing, consistent hashing requires only a relatively small amount of data to be moved: if you add a machine to the cluster, only the data that needs to live on that machine is moved there; all the other data stays where it is.
To understand how consistent hashing works, imagine wrapping the unit interval [tex][0,1)[/tex] onto a circle:
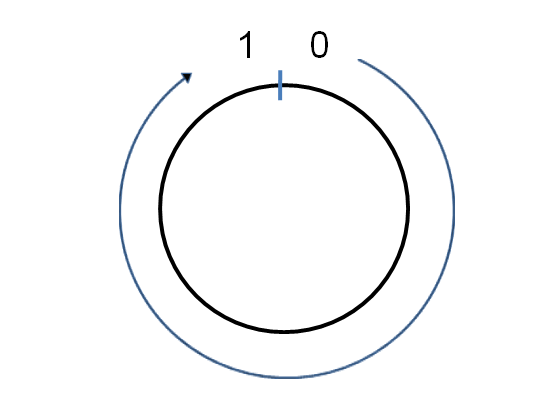
Suppose we number the machines [tex]0,\ldots,n-1[/tex]. If the hash function has range [tex][0,R)[/tex] then we rescale the hash function via [tex]x \rightarrow \mbox{hash}(x)/R[/tex], so that the hash function maps into the range [tex][0,1)[/tex], i.e., effectively onto the circle. Then we can hash machine number [tex]j[/tex] to a point [tex]\mbox{hash}(j)[/tex] on the circle, for each machine in the range [tex]j = 0,1,\ldots,n-1[/tex]. Here’s what it might look like for an [tex]n=3[/tex] machine cluster:
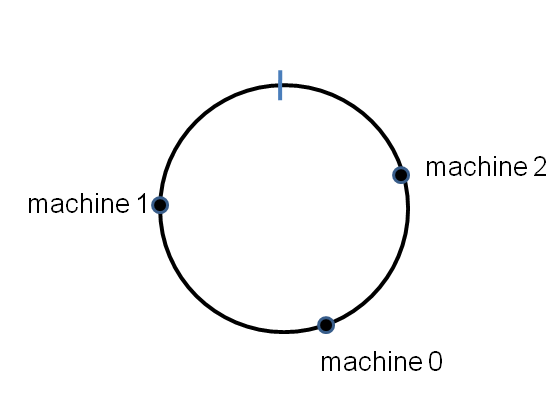
The points will be randomly distributed around the circle. Now suppose we have a key-value pair we want to store in the distributed dictionary. We simply hash the key onto the circle, and then store the key-value pair on the first machine that appears clockwise of the key’s hash point. E.g., for the key shown here, the key-value pair is stored on machine number [tex]1[/tex]:
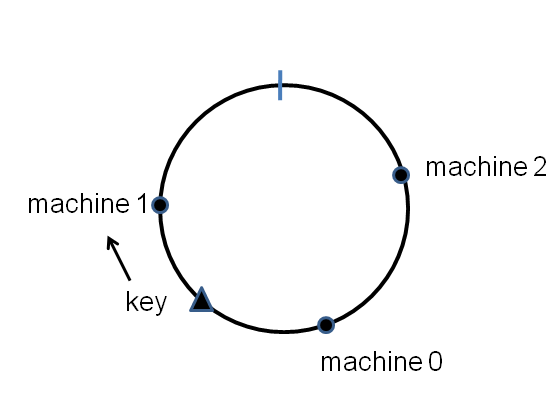
Because of the uniformity of the hash function, a fraction roughly [tex]1/n[/tex] of the key-value pairs will get stored on any single machine.
Now imagine we add an extra machine into the cluster. It goes to the point [tex]\mbox{hash}(n)[/tex]:
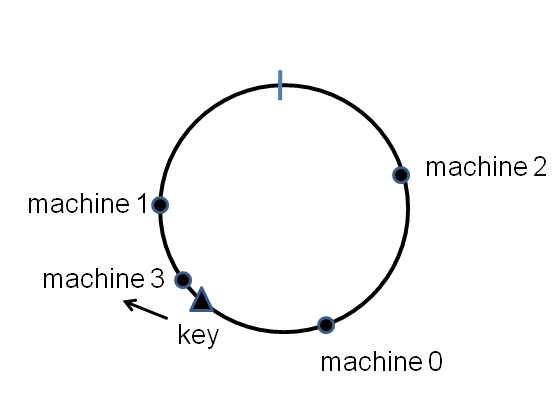
Most of the key-value pairs are completely unaffected by this change. But we can see that some of the key-value pairs that were formerly stored on machine [tex]1[/tex] (including our example key-value pair) will need to be moved to the new machine. But the fraction that needs to be moved will typically be [tex]1/(n+1)[/tex] of the total, a much smaller fraction than was the case for naive hashing.
The procedure I’ve described isn’t quite ideal, for a couple of reasons. First, the distribution of keys can be pretty irregular. If, for example, two of the machines – say [tex]j[/tex] and [tex]j'[/tex] – get mapped to very nearby points on the circle, then one of those machines may end up with very few of the keys, and some other machines with correspondingly more. It’s not that serious a problem, but why waste even a single machine? Second, when a machine is added to the cluster, all the keys redistributed to that machine come from just one other machine. Ideally, the keys would come in a more balanced way from several other machines.
Both these problems are easily resolved. Instead of mapping machine number [tex]j[/tex] to a single point on the circle, we’ll map it to multiple points (“replicas”). In particular, let’s imagine that for each machine we pick out [tex]r[/tex] points, by hashing [tex](j,0), (j,1),\ldots(j,r-1)[/tex] onto the circle. Otherwise, everything works exactly as before. By adding these replicas, we increase both the uniformity with which key-value pairs are mapped to machines, and also ensure that when a machine is added to the cluster, a smaller number of keys ([tex]\Theta(1/rn)[/tex]) are redistributed to that machine, from each of [tex]\Theta(r)[/tex] other machines in the cluster.
Here’s a simple Python program that implements consistent hashing. It’s largely self-explanatory; if you’d like to play around with it, I recommend reading the doc string for the ConsistentHash class.
'''consistent_hashing.py is a simple demonstration of consistent
hashing.'''
import bisect
import hashlib
class ConsistentHash:
'''ConsistentHash(n,r) creates a consistent hash object for a
cluster of size n, using r replicas.
It has three attributes. num_machines and num_replics are
self-explanatory. hash_tuples is a list of tuples (j,k,hash),
where j ranges over machine numbers (0...n-1), k ranges over
replicas (0...r-1), and hash is the corresponding hash value,
in the range [0,1). The tuples are sorted by increasing hash
value.
The class has a single instance method, get_machine(key), which
returns the number of the machine to which key should be
mapped.'''
def __init__(self,num_machines=1,num_replicas=1):
self.num_machines = num_machines
self.num_replicas = num_replicas
hash_tuples = [(j,k,my_hash(str(j)+"_"+str(k))) \
for j in range(self.num_machines) \
for k in range(self.num_replicas)]
# Sort the hash tuples based on just the hash values
hash_tuples.sort(lambda x,y: cmp(x[2],y[2]))
self.hash_tuples = hash_tuples
def get_machine(self,key):
'''Returns the number of the machine which key gets sent to.'''
h = my_hash(key)
# edge case where we cycle past hash value of 1 and back to 0.
if h > self.hash_tuples[-1][2]: return self.hash_tuples[0][0]
hash_values = map(lambda x: x[2],self.hash_tuples)
index = bisect.bisect_left(hash_values,h)
return self.hash_tuples[index][0]
def my_hash(key):
'''my_hash(key) returns a hash in the range [0,1).'''
return (int(hashlib.md5(key).hexdigest(),16) % 1000000)/1000000.0
def main():
ch = ConsistentHash(7,3)
print "Format:"
print "(machine,replica,hash value):"
for (j,k,h) in ch.hash_tuples: print "(%s,%s,%s)" % (j,k,h)
while True:
print "\nPlease enter a key:"
key = raw_input()
print "\nKey %s maps to hash %s, and so to machine %s" \
% (key,my_hash(key),ch.get_machine(key))
if __name__ == "__main__": main()
Having understood the basics of consistent hashing, there’s many natural followup questions: what’s the best way to cope with servers of different sizes; how to add and remove more than one machine at a time; how to cope with replication and fault-tolerance; how to migrate data when jobs are going on (including backups); and how best to backup a distributed dictionary, anyway? Hopefully it’s easy to get started on answering these questions at this point.
Let me finish up with a little background history. Consistent hashing was introduced pretty recently, in 1997, in a pair of papers, one describing the theory, the other about implementation. Note that the original papers were focused on applications to caching on the world wide web, not to distributed computing applications like MapReduce. A good (and funny!) basic introduction to consistent hashing is here. It’s now widely used inside services like the popular memcached caching system, and Amazon’s Dynamo key-value store.
About this post: This is one in a series of posts about the Google Technology Stack – PageRank, MapReduce, and so on. The posts are summarized here, and there is FriendFeed room for the series here. The posts are based on fortnightly meetups of a small group in Waterloo – email me (mn@michaelnielsen.org) if you’re local and interested in attending. Subscribe to my blog to follow future posts in the series.